蒙特卡罗方法验证出生率

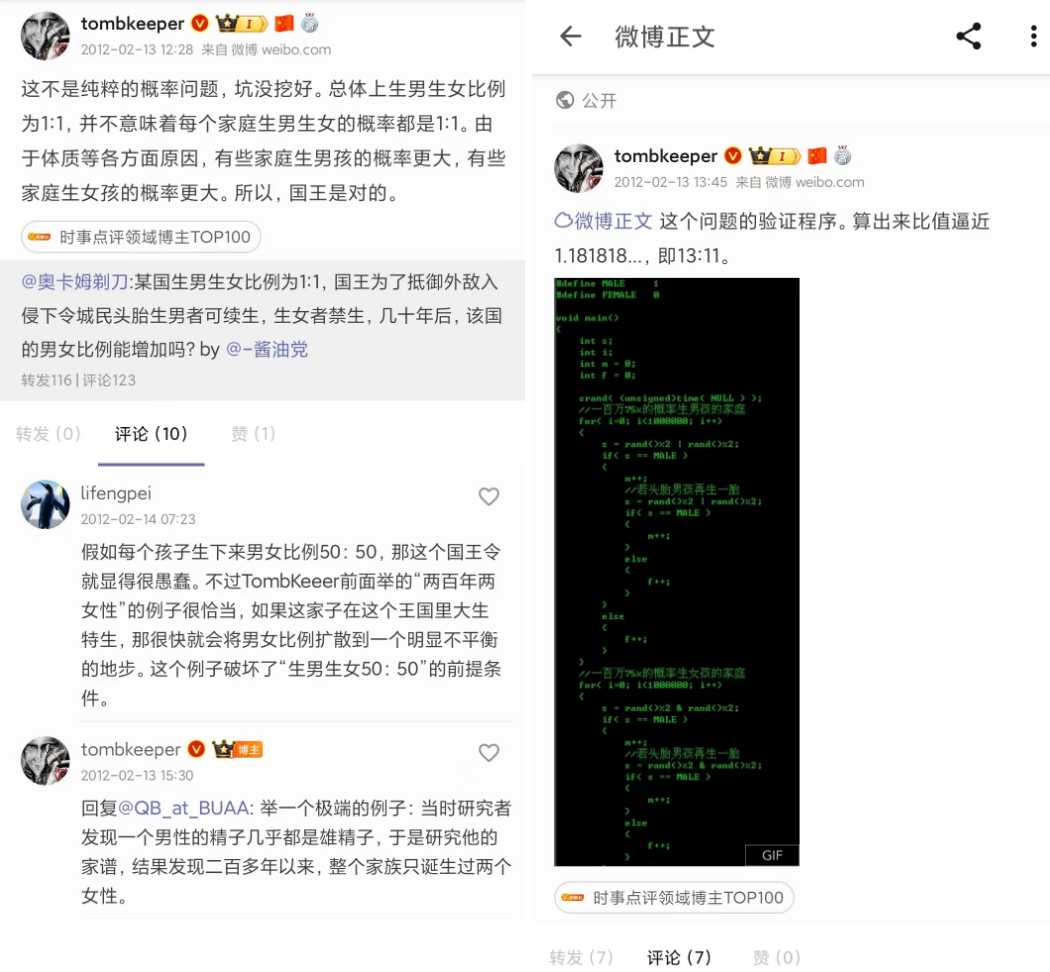
2012年2月，博主 @奥卡姆剃刀发表了一条微博

某国生男生女比例为1:1，国王为了抵御外敌入侵下令城民头胎生男者可续生，生女者禁生，几十年后，该国的男女比例能增加吗？

按照常理，这样的政策执行应该不会对人口比例造成影响，然而教主 @tombkeeper 却经过枚举验证，得到了不一样的结论

微博截图

源微博链接：https://weibo.com/1401527553/y5hUMDoD0

教主的验证代码由C语言编写，由于我尚未学习C语言，只能向ChatGPT求助。

\```C
#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define MALE 1
#define FEMALE 0

void main() {
    int s;
    int i;
    int m = 0;
    int f = 0;

    srand((unsigned)time(NULL));
    //一百万75%的概率生男孩的家庭
    for (i = 0 ; i < 1000000 ; i++) {
        s = rand() %2 | rand() %2;
        if (s == MALE) {
            m++;
            //若头胎男孩再生一胎
            s = rand() %2 | rand() %2;
            if (s == MALE) {
                m++;
            } else {
                f++;
            }
        } else {
            f++;
        }
    }

    //一百万75%的概率生女孩的家庭
    for (i = 0 ; i < 1000000 ; i++) {
        s = rand() %2 & rand() %2;
        if (s == MALE){
            m++;
            //若头胎男孩再生一胎
            s = rand() %2 & rand() %2;
            if (s == MALE) {
                m++;
            } else {
                f++;
            }
        } else {
            f++;
        }
    }

    printf("MALE:FEMALE = %d:%d\n", m, f);
}
\```

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

#define MALE 1
#define FEMALE 0

int main() {
    int s;
    int i;
    int m = 0;
    int f = 0;

    srand((unsigned)time(NULL));
    // 一百万75%的概率生男孩的家庭
    for (i = 0 ; i < 1000000 ; i++) {
        s = (rand() % 4) < 3 ? MALE : FEMALE; // 75% 的机会是 MALE
        if (s == MALE) {
            m++;
        } else {
            f++;
        }
    }

    // 一百万75%的概率生女孩的家庭
    for (i = 0 ; i < 1000000 ; i++) {
        s = (rand() % 4) < 3 ? FEMALE : MALE; // 75% 的机会是 FEMALE
        if (s == MALE){
            m++;
        } else {
            f++;
        }
    }

    printf("MALE:FEMALE = %d:%d\n", m, f);

    return 0;
}

上述代码中体现了这些知识点：

计算随机数的方法

在C语言中，rand() 函数返回的是一个随机整数，范围是从0到RAND_MAX，其中 RAND_MAX 是一个预定义的常数，在大多数系统上，它的值是32767。
按位运算

计算机的数值计算的底层逻辑，可以提高计算速度。它并不特定于任何一种语言，C和Java都支持位运算，并且它们的效率都是比较高的。但在这个特定的问题中，我们并不需要使用位运算，因为我们不是在处理位级别的操作，我们只是生成随机数并进行比较。
对概率的模拟

ChatGPT认为：rand() % 2 生成的是0或1，这意味着有50%的概率得到0或1。代码中使用了按位或（|）和按位与（&）操作符，实际上并没有改变这个概率。
蒙特卡罗算法

也称统计模拟方法，使用随机数（或更常见的伪随机数）来解决很多计算问题的方法。将所求解的问题同一定的概率模型相联系，用电子计算机实现统计模拟或抽样，以获得问题的近似解。

同时，ChatGPT也使用Java语言重写了上面的代码

public class GenderRatio {

    static final int MALE = 1;
    static final int FEMALE = 0;

    public static void main(String[] args) {
        int s;
        int m = 0;
        int f = 0;

        // 一百万75%的概率生男孩的家庭
        for (int i = 0; i < 1000000; i++) {
            s = ((int) (Math.random() * 4) < 3) ? MALE : FEMALE;
            if (s == MALE) {
                m++;
                s = ((int) (Math.random() * 4) < 3) ? MALE : FEMALE;
                if (s == MALE) {
                    m++;
                } else {
                    f++;
                }
            } else {
                f++;
            }
        }

        // 一百万75%的概率生女孩的家庭
        for (int i = 0; i < 1000000; i++) {
            s = ((int) (Math.random() * 4) < 3) ? FEMALE : MALE;
            if (s == MALE) {
                m++;
                s = ((int) (Math.random() * 4) < 3) ? FEMALE : MALE;
                if (s == MALE) {
                    m++;
                } else {
                    f++;
                }
            } else {
                f++;
            }
        }

        System.out.printf("MALE:FEMALE = %d:%d\n", m, f);
    }
}