LeetCode刷题笔记

掌握数据结构和算法逻辑

很多时候感觉到自己的思路不够清晰，在刷题时看到其他人的题解才发现自己的不足

在while循环和if判断条件搭配使用时，需要清楚地认识到：if语句如果没有改变循环判断条件中的值，那么在if执行结束后，循环会在之前的位置上重新循环，而不会像for循环那样跳到下一处

栈的Java实现：Stack，ArrayDeque，LinkedList的区别_stack,arraydeque,linkedlist 的区别-CSDN博客

复杂度比较

复杂度比较公式： $O(1)<O(\log n)<O(\sqrt{n})<O(n)<O(n\log n)<O(n^2)<O(2^n)<O(n!)$

在常数时间下，访问速度：位运算>算术运算>寻址>Hash函数
链表属于跳转结构，消耗的不是常数时间

复杂度和控制结构的写法无关

只有一个循环，可以实现 O(n²) 的时间复杂度，例如while循环实现的冒泡排序

public static void bubbleSort(int[] arr) {
	if (arr == null || arr.length < 2) {
		return;
	}
	int n = arr.length;
	int end = n - 1, i = 0;
	while (end > 0) {
		if (arr[i] > arr[i + 1]) {
			int tmp = arr[i];
               arr[i] = arr[i + 1];
               arr[i + 1] = tmp;
		}
		if (i < end - 1) {
			i++;
		} else {
			end--;
			i = 0;
		}
	}
}

两个for循环，通过不同的循环条件，可以实现O(log(n)) 和 O(n²) 两种时间复杂度

int N = 200000;
long start;
long end;
System.out.println("测试开始");
start = System.currentTimeMillis();
for (int i = 1; i <= N; i++) {
	for (int j = i; j <= N; j += i) {
		// 这两个嵌套for循环的流程，时间复杂度为O(N * logN)
		// 1/1 + 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/n，也叫"调和级数"，收敛于O(logN)
		// 所以如果一个流程的表达式 : n/1 + n/2 + n/3 + ... + n/n
		// 那么这个流程时间复杂度O(N * logN)
	}
}
end = System.currentTimeMillis();
System.out.println("测试结束，运行时间 : " + (end - start) + " 毫秒");

System.out.println("测试开始");
start = System.currentTimeMillis();
for (int i = 1; i <= N; i++) {
	for (int j = i; j <= N; j++) {
		// 这两个嵌套for循环的流程，时间复杂度为O(N^2)
		// 很明显等差数列
	}
}
end = System.currentTimeMillis();
System.out.println("测试结束，运行时间 : " + (end - start) + " 毫秒");

平均时间复杂度

严格固定流程的算法，一定强调最差情况（比如插入排序）；算法流程上利用随机行为作为重要部分的，要看平均或者期望的时间复杂度，因为最差的时间复杂度无意义

// 随机生成长度为n
// 值在0~v-1之间
// 且任意相邻两数不相等的数组
int n = 10;
int v = 4;
int[] arr1 = new int[n];
arr1[0] = (int) (Math.random() * v);
for (int i = 1; i < n; i++) {
	do {
		arr1[i] = (int) (Math.random() * v);
	} while (arr1[i] == arr1[i - 1]);
}
for (int num : arr1) {
	System.out.print(num + " ");
}
System.out.println();
System.out.println("=========");

上面的算法最差时间复杂度是正无穷，但是在大数据下没有意义，在计算时考虑的是平均复杂度

各个语言中的动态数组的初始大小和实际扩容因子可能会变化，但是均摊都是O(1)，例如Java中的动态数组ArrayList

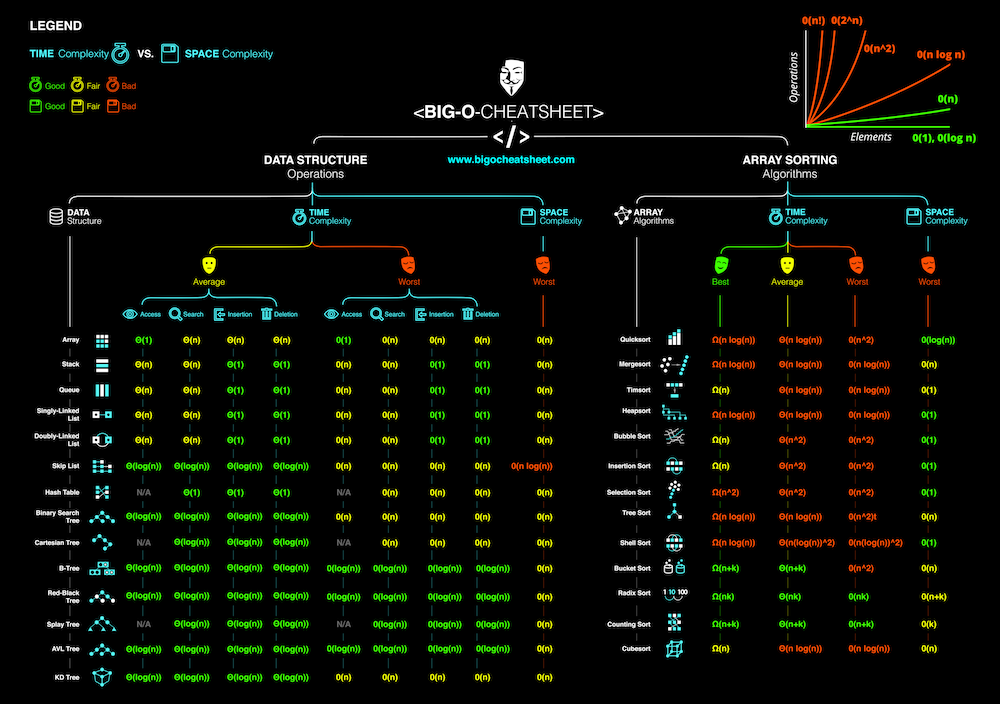
不同数据结构、排序算法对应的时间、空间复杂度

数据结构、算法复杂度对比图

常用的数据结构时间、空间复杂度

Data Structure	Time Complexity	时间复杂度	Time Complexity	时间复杂度	Time Complexity	时间复杂度	Time Complexity	时间复杂度	Space Complexity
	Average	平均	Average	平均	Worst	最差	Worst	最差	Worst最差
	Access 访问	Search 查找	Insertion 插入	Deletion 删除	Access 访问	Search 查找	Insertion 插入	Deletion 删除
数组 Array	Θ(1)	Θ(n)	Θ(n)	Θ(n)	O(1)	O(n)	O(n)	O(n)	O(n)
栈 Stack	Θ(n)	Θ(n)	Θ(1)	Θ(1)	O(n)	O(n)	O(1)	O(1)	O(n)
队列 Queue	Θ(n)	Θ(n)	Θ(1)	Θ(1)	O(n)	O(n)	O(1)	O(1)	O(n)
单向链表 Singly-Linked List	Θ(n)	Θ(n)	Θ(1)	Θ(1)	O(n)	O(n)	O(1)	O(1)	O(n)
双向链表 Doubly-Linked List	Θ(n)	Θ(n)	Θ(1)	Θ(1)	O(n)	O(n)	O(1)	O(1)	O(n)
跳表 Skip List	Θ(log(n))	Θ(log(n))	Θ(log(n))	Θ(log(n))	O(n)	O(n)	O(n)	O(n)	O(n log(n))
哈希表 Hash Table	N/A	Θ(1)	Θ(1)	Θ(1)	N/A	O(n)	O(n)	O(n)	O(n)
二叉搜索树 Binary Search Tree	Θ(log(n))	Θ(log(n))	Θ(log(n))	Θ(log(n))	O(n)	O(n)	O(n)	O(n)	O(n)
笛卡尔树 Cartesian Tree	N/A	Θ(log(n))	Θ(log(n))	Θ(log(n))	N/A	O(n)	O(n)	O(n)	O(n)
B树 B-Tree	Θ(log(n))	Θ(log(n))	Θ(log(n))	Θ(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(n)
红黑树 Red-Black Tree	Θ(log(n))	Θ(log(n))	Θ(log(n))	Θ(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(n)
伸展树 Splay Tree	N/A	Θ(log(n))	Θ(log(n))	Θ(log(n))	N/A	O(log(n))	O(log(n))	O(log(n))	O(n)
AVL树 AVL Tree	Θ(log(n))	Θ(log(n))	Θ(log(n))	Θ(log(n))	O(log(n))	O(log(n))	O(log(n))	O(log(n))	O(n)
K-D树 KD Tree	Θ(log(n))	Θ(log(n))	Θ(log(n))	Θ(log(n))	O(n)	O(n)	O(n)	O(n)	O(n)

常用的排序算法时间、空间复杂度

Algorithm	Time Complexity	Time Complexity	Time Complexity	Space Complexity
	Best	Average	Worst	Worst
快速排序 Quicksort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n^2)`	`O(log(n))`
归并排序 Mergesort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n log(n))`	`O(n)`
Timsort	`Ω(n)`	`Θ(n log(n))`	`O(n log(n))`	`O(n)`
堆排序 Heapsort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n log(n))`	`O(1)`
冒泡排序 Bubble Sort	`Ω(n)`	`Θ(n^2)`	`O(n^2)`	`O(1)`
插入排序 Insertion Sort	`Ω(n)`	`Θ(n^2)`	`O(n^2)`	`O(1)`
选择排序 Selection Sort	`Ω(n^2)`	`Θ(n^2)`	`O(n^2)`	`O(1)`
树形排序 Tree Sort	`Ω(n log(n))`	`Θ(n log(n))`	`O(n^2)`	`O(n)`
希尔排序 Shell Sort	`Ω(n log(n))`	`Θ(n(log(n))^2)`	`O(n(log(n))^2)`	`O(1)`
桶排序 Bucket Sort	`Ω(n+k)`	`Θ(n+k)`	`O(n^2)`	`O(n)`
基数排序 Radix Sort	`Ω(nk)`	`Θ(nk)`	`O(nk)`	`O(n+k)`
计数排序 Counting Sort	`Ω(n+k)`	`Θ(n+k)`	`O(n+k)`	`O(k)`
Cubesort	`Ω(n)`	`Θ(n log(n))`	`O(n log(n))`	`O(n)`